Faraday's laws of electrolysis

Faraday's laws of electrolysis are quantitative relationships based on the electrochemical researches published by Michael Faraday in 1834

Statements of the laws

Several versions of the laws can be found in textbooks and the scientific literature. The most common statements resemble the following:

Faraday's 1st Law of Electrolysis - The mass of a substance altered at an electrode during electrolysis is directly proportional to the quantity of electricity transferred at that electrode. Quantity of electricity refers to the quantity of electrical charge, typically measured in coulomb.

Faraday's 2nd Law of Electrolysis - For a given quantity of D.C electricity (electric charge), the mass of an elemental material altered at an electrode is directly proportional to the element's equivalent weight. The equivalent weight of a substance will be explained in the next paragraph.

For an element the equivalent weight is the quantity that combines with or replaces 1.00797 grams (g) of hydrogen or 7.9997 g of oxygen; or, the weight of an element that is liberated in an electrolysis (chemical reaction caused by an electric current) by the passage of 9.64853399(24) x 104 coulombs of electricity. The equivalent weight of an element is its gram atomic weight divided by its valence (combining power). Some equivalent weights are: silver (Ag), 107.868 g; magnesium (Mg), 24.312/2 g; aluminum (Al), 26.9815/3 g; sulfur (S, in forming a sulfide), 32.064/2 g. For compounds that function as oxidizing or reducing agents (compounds that act as acceptors or donors of electrons), the equivalent weight is the gram molecular weight divided by the number of electrons lost or gained by each molecule; e.g., potassium permanganate (KMnO4) in acid solution, 158.038/5 g; potassium dichromate (K2Cr2O7), 294.192/6 g; and sodium thiosulfate (Na2S2O3·5H2O), 248.1828/1 g. For all oxidizing and reducing agents (elements or compounds) the equivalent weight is the weight of the substance that is associated with the loss or gain of 6.023 × 10^23 electrons. The equivalent weight of an acid or base for neutralization reactions or of any other compound that acts by double decomposition is the quantity of the compound that will furnish or react with or be equivalent to 1.00797 g of hydrogen ion or 17.0074 g of hydroxide ion; e.g., hydrochloric acid (HCl), 36.461 g; sulfuric acid (H2SO4), 98.078/2 g; sodium hydroxide (NaOH), 40 g; sodium carbonate (Na2CO3), 105.9892/ 2 g. The equivalent weight of a substance may vary with the type of reaction it undergoes. Thus, potassium permanganate reacting by double decomposition has an equivalent weight equal to its gram molecular weight, 158.038/1 g; as an oxidizing agent under different circumstances it may be reduced to the manganate ion (MnO42-), to manganese dioxide (MnO2), or to the manganous ion (Mn2+), with the equivalent weights of 158.038/1 g, 158.038/3 g, and 158.038/5 g, respectively. The number of equivalent weights of any substance dissolved in one litre of solution is called the normality of that solution.

Mathematical form

Faraday's laws can be summarized by

where:

• m is the mass of the substance liberated at an electrode in grams
• Q is the total electric charge passed through the substance
• F = 96485 C mol⁻¹ is the Faraday constant
• M is the molar mass of the substance
• z is the valency number of ions of the substance (electrons transferred per ion).

Note that M/z is the same as the equivalent weight of the substance altered.

For Faraday's first law, M, F, and z are constants, so that the larger the value of Q the larger m will be.

For Faraday's second law, Q, F, and z are constants, so that the larger the value of M/z (equivalent weight) the larger m will be.

In the simple case of constant-current electrolysis, 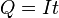 le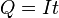ading to

and then to

where:

• n is the amount of substance ("number of moles") liberated: n = m/M
• t is the total time the constant current was applied.

In the more complicated case of a variable electrical current, the total charge Q is the electric current I() integrated over time :

Here t is the total electrolysis time.

This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

Posted in: STUDENT'S AREA